What is CRRA Utility Function: Explained in 6 Easy Steps

In this post, you’ll learn what is CRRA utility function (also called power utility function). We’ll go over 6 things you must know to understand the CRRA formula and the CRRA utility function properties.

CRRA stands for Constant Relative Risk Aversion.

Constant Relative Risk Aversion is when relative risk aversion is the same at every wealth level.

Let’s start by understanding risk aversion:

#1) Risk Aversion

Risk aversion is the tendency investors have to prefer certainty over uncertainty. They prefer lower returns with known risks over higher returns with unknown risks.

We want to measure an investor’s aversion to risk. Why? Because this allows us to compare if one investor is more risk averse than another, and to understand how an investor’s risk aversion affects his investment behavior (how does he choose the assets that compose his portfolio).

Investors’ risk aversion will affect the demand for financial assets, which in turn has an impact on the price of these assets.

A risk averse investor will avoid a fair bet. What is a fair bet? One whose expected value is zero.

For example, would you take a bet where you have a 50% chance of winning $10,000 and a 50% chance to lose $10,000? This is a fair bet. Its expected value is 10,000×0.5+(-10,000)x0.5=0. A rational being would take this bet, yet, most people will avoid it.

However, will a person with a million dollars in their bank account avoid this bet? Probably not. They don’t care as much so they would take the bet, because losing 10k is not as bad to them.

Now, what if the bet is in proportion to your wealth? Say 50%. It’s safe to say everyone, no matter how rich or poor, will likely avoid this bet. They have the same relative risk aversion.

In this case, the gain or loss of a bet is measured in terms of the initial wealth of the investor, instead of an absolute value.

Now, some people are more risk averse than others, depending on their utility function:

#2) Utility Function

What is a utility function?

Your utility function measures the satisfaction you get from different bundles of goods, services, or investments.

Risk aversion also means we prefer smooth consumption. We want to save some of our consumption from periods of abundance to periods of scarcity to get more stability and predictability.

We get a bigger benefit from consuming something moderately over time, over consuming it all at once and then having nothing. Whatever it is. Even though we consumed the same amount.

A good utility function will reflect the human tendency to be risk averse. How? By being concave:

#3) Second Derivative of a Concave Function

The richer you are, the less you care, and hence are less risk averse. A concave function reflects this because it has a progressively lower slope of the tangent line. In other words, it has decreasing marginal utility. This slope is the first derivative of said function.

Positive deviations in a concave function do not help as much as negative ones hurt. This means for a risk averse investor with a concave utility, the joy of making money is smaller than the pain of losing the same amount.

For lower levels of wealth, the utility you get from a positive variation in wealth is bigger than the utility someone with a higher level of wealth gets.

Now, let’s understand derivatives:

The derivative of a function is its instantaneous rate of change.

The derivative of a function f(X) = Y tells you how a change in X relates to the change in Y.

For example, let’s say the derivative of function f(X) is 5 when X is 1000. Hence, f(1000) = 5. If X increases by 1 (from 1000 to 1001), Y will increase by 5. This means f(1000+1) = Y + 5.

Let’s say a function gives you distance.

The 1^st derivative is the rate of change in distance, so your speed.

The 2^nd derivative is the rate of change in speed, so your acceleration.

A utility function with a negative second derivative implies risk aversion.

As wealth increases, the slope of the tangent lines of the utility function is smaller and smaller. This means “speed” is decreasing and the 2^nd derivative is negative.

As “acceleration” becomes less negative (because speed is approaching zero—even though it’s still positive) investors are less risk averse.

In other words, a good utility function will have positive (U’ > 0) but decreasing (U” < 0) marginal utility.

Now, you can’t say investor A is more risk averse than investor B simply because the absolute value of acceleration is higher. You need a measure that is not affected by affine transformations.

With that in mind, we have two ways to measure risk aversion:

• Absolute Risk Aversion.
• Relative Risk Aversion.

We’ve touched on this briefly. Now let’s dive deeper:

#4) Absolute Risk Aversion Coefficient

The absolute risk aversion coefficient is the second derivative of the utility function divided by its first derivative:

\[\alpha(w)=-\frac{u”(w)}{u'(w)}\]

We represent it with the Greek letter alpha (α). The w between parentheses means wealth, and it illustrates utility may depend on wealth. There are some cases where it is constant, though. The minus sign in the beginning serves the sole purpose of making the result positive, since the second derivative is always negative for a concave function.

For any risk averse investor, the absolute risk aversion coefficient is positive.

The higher his measure of absolute risk aversion, the more favorable odds the investor demands to be willing to accept an investment.

By dividing the first derivative by the second, the coefficient of absolute risk aversion is unaffected by monotone affine transforms of the utility function. It will give you the exact same risk coefficient regardless of these transformations.

Why is this important?

Utility must depend on the investors’ preferences and not on the particular utility function representing the preferences.

For decisions under uncertainty, utility functions are unique (meaning they represent different preferences) up to monotone affine transforms.

If two utility functions u and f represent the same preferences over all wealth gambles, then u must be a monotone affine transform of f. u and f are the same utility function. Both uniquely characterize the same investor.

As opposed to affine transformations (which are linear), a non-linear transformation (logarithmic transformation, for example) does not always respect the preferences ranking that the utility function it is applied to represents.

Again, even though its name is “absolute,” we can’t just look at the absolute value of the acceleration of the utility function (2^nd derivative) to judge its level of risk aversion.

If you’re having trouble visualizing what is a function’s transformation, the example at the end should help clarify things.

#5) Relative Risk Aversion Coefficient

The relative risk aversion coefficient is the absolute risk aversion coefficient multiplied by the level of wealth. It is represented by the Greek letter rho (ρ).

\[\rho(w)=w\alpha(w)=-\frac{wu”(w)}{u'(w)}\]

Everything we saw for the absolute coefficient still applies. The only difference is that risk aversion no longer depends on how rich or poor the investor is.

Risk aversion will be the same irrespective of the level of wealth.

Remember proportional bets? This coefficient measures risk aversion in those cases.

Understanding what is the CRRA utility function should be easier now:

What is CRRA Utility Function?

A utility function has Constant Relative Risk Aversion (CRRA) when its risk aversion measure has the same value for all levels of wealth.

The CRRA function is also known as the Power Utility Function, and it takes this form:

\[u(w)=\begin{cases}\frac{w^{1-\rho}}{1-\rho} & \rho>0, \rho \neq1\\ln(w) & \rho = 0\end{cases}\]

Any CRRA utility function is a monotone affine transform of one of these.

Even though it says “constant relative”, we can still talk about absolute:

Any CRRA utility function has decreasing absolute risk aversion. α(w) = ρ(w)/w
means as wealth increases in the denominator, the absolute risk aversion coefficient becomes smaller.

ρ is the coefficient of relative risk aversion of the power utility function.

If 2 investors have different CRRA utility functions, the one with the higher value of ρ is more risk averse.

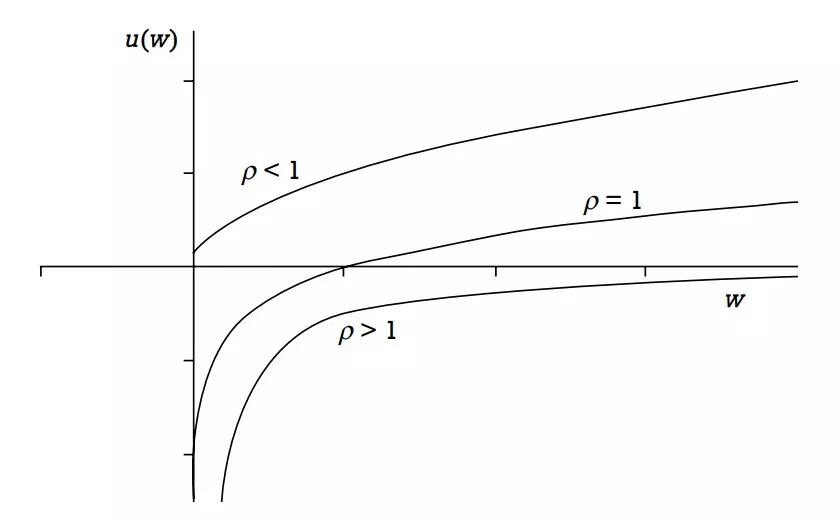
An investor with power utility is more risk averse than a log-utility investor if ρ > 1 and less risk averse if ρ < 1. The higher the ρ, the less the investor is willing to pay to play a gamble (this value he’s willing to pay is called the certainty equivalent).

An increasing certainty equivalent means you are less risk averse and ρ is lower.

Opposed to the certainty equivalent, there’s the risk premium. This value is sort of like insurance and tells you how much an investor is willing to pay to avoid the gamble. The more risk averse he is, the more he’ll pay.

Difference between CARA and CRRA

The Constant Relative Risk Aversion (CRRA) utility function has the same level of relative risk aversion for every wealth level.

This means the fraction of wealth a CRRA-utility investor would pay to avoid a gamble (this gamble is also proportional to initial wealth) is independent of their wealth.

There is also Constant Absolute Risk Aversion (CARA). Constant Absolute Risk Aversion is when absolute risk aversion is the same at every wealth level.

Every CARA utility function is a monotone affine transform of the exponential utility function. Here’s the CARA utility function formula:

\[u(w)=-e^{-\alpha w}\]

This is an exponential utility function, and the absolute risk aversion coefficient is equal to the coefficient (α) of w in the exponent.

So, the CARA utility function also implies the same risk aversion at every wealth level. The difference is in how much the investor is willing to pay to play the bet.

With CARA, it is not a value relative to the money the investor already has, but a constant value.

Thus, someone with CARA utility will pay the same risk premium to avoid a fair gamble no matter what her initial wealth might be. This is unrealistic. Here’s why:

Consider flipping a fair coin for $1,000. The amount an individual with CARA utility would pay to avoid the gamble is the same whether she starts with a wealth of $1,000 or a wealth of $1,000,000,000.

In reality, if she’s a billionaire the gamble is insignificant. Since it is a fair gamble (expected value is zero), the investor will pay very little to avoid it. On the other hand, she might pay a significant amount to avoid gambling all of her wealth.

If an investor would pay less with an initial wealth of $1,000,000,000 than with an initial wealth of $1,000 to avoid the gamble—then she has CRRA utility. If she would pay the same, she has CARA utility.

CRRA utility looks at if the gamble was for example 5% of the investor’s wealth. So, flipping a coin for $50 if you have a net worth of $1,000. And for $50,000,000 if you have a net worth of a billion.

In this case, both investors will do the same—whatever it is (play or not)—because the money at stake is proportional to how much they already have.

Constant Relative Risk Aversion is more realistic.

Read also: Quadratic Utility Function (Mean-Variance Preferences): Is It Realistic?

Now, you can only compare risk aversion between investors when they have the same utility function. A lot of times, you will be given a function that can be rewritten as the power utility function, as it is an affine transformation of it. This allows you to get to the relative risk aversion coefficient and compare results.

Let’s look at a power utility function example:

Constant Relative Risk Aversion Utility Function Example

An investor’s current wealth is $100,000. He’s faced with the following gamble (also called lottery). Win $50,000 with 50% chance, or win $10,000 with 50% chance.

He can’t lose, can he? Well, we know. What we want to see is how much is he willing to pay to play this gamble. What is the maximum value he’s willing to give up to get in on this bet?

In other words, what is the value that if he received with 100% chance, would make him indifferent to this lottery?

In yet another set of words, what is the certainty equivalent?

The utility function that describes his risk aversion is:

\[u(w)=-\frac{1}{w}\]

He has two buddies. They have the same initial wealth of 100k. The difference is the utility function of investor B utility function is:

\[u(w)=\ln w\]

And of C is:

\[u(w)=\frac{w^{0.3}}{0.3}\]

The certainty equivalent for investor A is extrapolated from the following equality:

\[-\frac{1}{100000+50000}\times0.50+(-\frac{1}{100000+10000})\times0.5=-\frac{1}{100000+CE}\]

Thus, the certainty equivalent (CE) is $26,923.

For investor B:

\[\ln (100000+50000)\times0.5+\ln (100000+10000)\times0.5=\ln (100000+CE)\]

The certainty equivalent is $28,452.

And for C:

\[\frac{(100000+50000)^{0.3}}{0.3}\times0.5+\frac{(100000+10000)^{0.3}}{0.3}\times0.5=\frac{(100000+CE)^{0.3}}{0.3}\]

The certainty equivalent is $28,916.

Do you see how the certainty equivalent is increasing? Here’s why this is happening:

If you notice, all three functions are monotone affine transformations of the power utility.

This means we can rewrite them to get the relative risk aversion coefficient and compare the risk aversion of these three buddies.

For investor A:

\[u(w)=-\frac{1}{w}=-w^{-1}=\frac{w^{1-2}}{1-2}\]

This means the relative risk aversion coefficient for investor A is ρ = 2.

For investor B, we saw that when ρ = 1 we take the logarithmic utility function, which is his function in this case.

For investor C, ρ = is 0.70, as shown below:

\[u(w)=\frac{w^{0.3}}{0.3}=\frac{w^{1-0.7}}{1-0.7}\]

Notice that as the risk aversion coefficient becomes smaller, the corresponding certainty equivalent increases.

The main conclusion of this example is this:

As your risk aversion decreases, you are willing to pay more to play a given lottery.

The more risk averse you are, the higher of a value (certainty equivalent) you demand to become indifferent to playing the gamble or not.