The certainty equivalent of a lottery is the amount you would accept to receive to pass on the possibility of playing said lottery. In other words, it’s the maximum amount a person is willing to pay for a gamble. You find it by solving the equation that says the utility of your current wealth plus the certainty equivalent is equal to the expected utility from adding the lottery to your current wealth.
Still confused? Keep reading.
We’ll start by understanding what is the certainty equivalent, how utility functions determine each investor’s certainty equivalent (and risk premium), and finally how to how to calculate certainty equivalent cash flow (with an example).
Ready? Let’s dive in:
Certainty Equivalent Definition
The certainty equivalent (CE) is the maximum value an investor is willing to pay to enter a gamble. It’s also called equivalent risk-free return.
It varies from person to person, according to their utility function and how risk-averse they are.
The higher the certainty equivalent the investor requires, the higher his risk aversion is. Why?
The certainty equivalent is basically how much you’re willing to receive with 100% certainty that would make you choose that over playing a gamble.
For example, would you flip a coin if—heads you get $5, tails you get $0… Or would you rather receive $2 straight up?
$2 is the certainty equivalent. For some people it will be lower, which means they’re more comfortable with the uncertainty of the coin flip. For others it’ll be higher, as they prefer certain results.
The certainty equivalent is not a coefficient. Again, it is the guaranteed amount an agent is willing to accept instead of taking on risk. It’s the amount they value certainty over uncertainty.
Now, what determines the level of risk aversion of an investor? How can you measure it?
Utility functions.
Understanding Utility Functions
An utility function is a mathematical representation of an individual’s preferences throughout different levels of wealth or consumption.
It assigns a numerical value to each possible outcome, reflecting the individual’s subjective satisfaction (or “utility”) from that outcome.
Utility functions allow you to compare whether one investor is more risk-averse than another and understand how an investor’s risk aversion affects his investment behavior and the composition of their portfolio.
Similarly to how a quadratic equation is written as f(x), an utility function is usually written as u(w).
Humans are risk-averse. We prefer outcomes with low uncertainty over those with high uncertainty, even when higher risk means higher expected value.
You would rather get $100 than take a 50/50 chance of receiving either $200 or $0, right? Well, the expected value of both options is $100.
To reflect this in a function, it needs to be concave. Why?
Because people experience diminishing marginal utility as their wealth increases. Each additional dollar provides less satisfaction than the previous one.
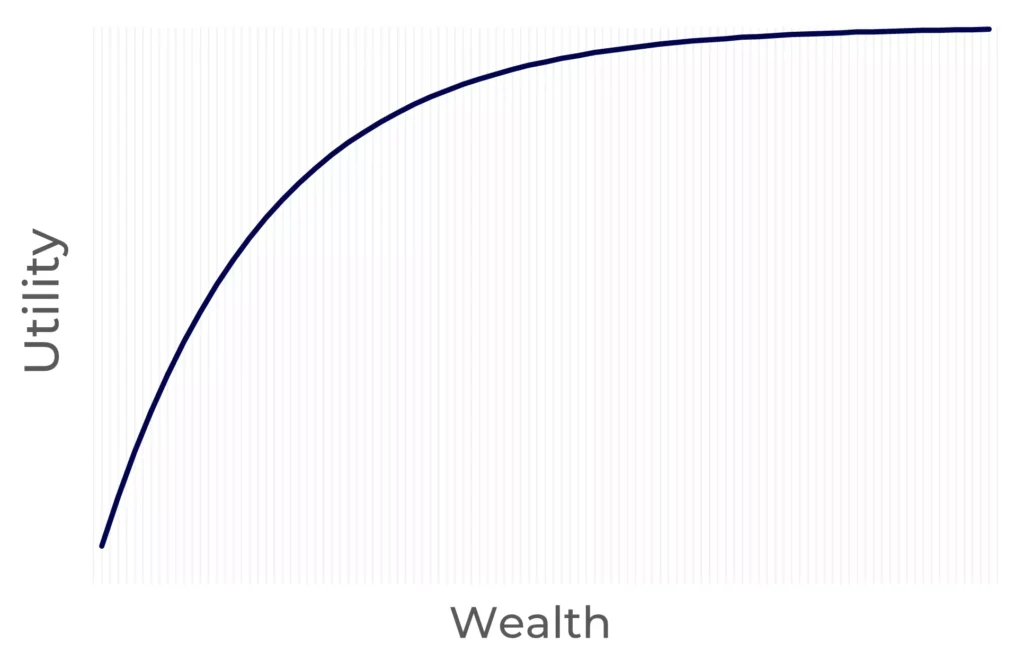
A concave function has a negative second derivative, which means its curvature is downward-facing. This reflects the idea that—as wealth increases, the additional satisfaction gained from more wealth decreases at a faster rate. In other words, the marginal utility of wealth is decreasing.
This implies investors may be willing to pay a premium (in terms of lower expected returns) to avoid uncertain outcomes and reduce their exposure to risk.
This is where the concept of risk premium comes in—the highest amount an investor is willing to pay to avoid a gamble.
The risk premium is the difference between the expected value of the bet and the certainty equivalent.
For example, if you have a 50% chance of winning $100 and 50% probability of losing $50, the expected value of the bet is 0.5×100+0.5x(-50)=$25. If you’re willing to accept 20 guaranteed dollars instead of taking the uncertain debt, that is your certainty equivalent. And the difference between $25 and $20? The risk premium.
It means you require an additional return of 25-20=$5 to compensate for taking on the risk. This implies you’re willing to pay $5 in order to avoid the gamble.
There are relative risk aversion and absolute risk aversion coefficients that help you measure the degree to which an investor is willing to trade off expected return for a reduction in risk.
The higher the risk aversion, the more favorable odds the investor will demand to accept a gamble.
Let’s look at how to calculate certainty equivalent from utility function:
How to Calculate Certainty Equivalent and Risk Premium
To find the certainty equivalent, you must solve the following equation for the CE:
Where:
- w is initial wealth. The current wealth the investor has.
- CE is the certainty equivalent. The money that gives the investor the same utility as the expected utility of a gamble that pays a random amount. This will be the unknown variable in the equation.
- Z̃ is a lottery. The uncertain risky payoff.
- u(w+CE) is the utility the investor gets from their initial wealth plus the certainty equivalent.
- Ε(u(w+Z̃)) is the sum of the expected utility of all lottery possibilities. In other words, a weighted average of the utilities of the uncertain payoffs, using the probability of the states of nature as weights.
This certainty equivalent formula is the same as subtracting the risk premium from the expected value of the lottery:
Where:
- π is the risk premium. Or the additional return an individual requires to compensate them for taking on risk. You can calculate it with the certainty equivalent and expected value.
Now that you know how to find certainty equivalent, let’s go through a quick example to put these concepts in motion:
Certainty Equivalent Lottery Example
Imagine an investor with the following utility function:
This is the exponential utility function (or Constant Absolute Risk Aversion utility function).
The investor has the possibility to play the lottery Z̃=(2, 0, 0.5). Her initial wealth w0 is 5.
Side note: The L=(h, -b, π) notation is Lottery=(Amount you can win, Amount you can lose, Probability of winning). So the higher the π, the higher the chance to win. For example, (1, -1, 0.6) would mean you can gain 1 with a 60% chance or lose 1 with a 40% chance.
In our example, the investor has equal probabilities of winning 2 or losing 0.
Now, how to calculate the certainty equivalent?
Using the certainty equivalent equation, we have:
As we’ve seen, on the left side you have u(w+CE) instead of u(w). Then, you equal that to the expected value of wealth after accounting for both of the lottery outcomes.
And the CE is the variable you’re trying to find by solving the whole equation.
The certainty equivalent of 0.5662 means the investor is willing to pay 0.5662 in order to play the lottery.
If you also want to know the risk premium, you simply subtract the certainty equivalent from the expected value of the lottery:
This means the investor requires an additional return of 0.4230 to compensate them for taking on the lottery’s risk.
Another way to look at it is:
If there was an insurance policy that, together with the original gamble, would guarantee the investor the expected pay-off of the gamble, what is the maximum premium he would be willing to pay for that insurance? It’s the risk premium value of 0.4230.
Key Takeaways (FAQs)
What is the certainty equivalent value?
The certainty equivalent of a gamble is the amount of money that gives you equal utility (meaning benefit, or satisfaction) to the random payoff of the gamble. If your certainty equivalent is lower than the expected value of the gamble, you are a risk averse person.
How do you find the certainty equivalent?
You extract it from an equation that equals the expected utility from adding the lottery to your initial wealth to the utility of your initial wealth plus the certainty equivalent. Or you can also do the expected value of the lottery minus the risk premium.
First, calculate the expected utility of the risky investment by weighting each possible outcome by its probability and then calculating the overall expected utility. Secondly, determine the certainty equivalent—the guaranteed return an individual is willing to accept as opposed to taking the risky asset. Finally, calculate the risk premium as follows: Risk Premium = Expected Utility of Risky Bet – Utility of Certainty Equivalent. In other words, it is equal to how much additional expected utility an individual requires to take on a risky bet instead of receiving a guaranteed payment (the certainty equivalent).
