The expanded net present value (ENPV) is the total value of a project, including the value of being able to adapt to new market conditions. It is equal to the NPV of the investment plus the value of real options.
The ability to expand, abandon, simply delay, or make any change to a project with the goal of adapting to (future) market conditions has value. This value is not captured in the conventional NPV.
For example, a project can have a negative conventional NPV and still be profitable because of its option to expand in the future.
Thus, the expanded NPV is a modified version of the traditional net present value financial analysis technique. What’s the difference? It takes into account managerial flexibility.
Still confused? Keep reading.
We’ll start by understanding the limitations of the conventional NPV analysis, explore the advantages of the expanded NPV, and look at an example of how to use it in practice.
Let’s dive right in:
The Problem with the Conventional NPV
The NPV is used in capital budgeting and investment planning to analyze the profitability of a projected investment or project.
Under the discounted cash flow model in capital budgeting, managers should accept a project if the value it creates surpasses its costs. The goal? To maximize shareholders’ wealth.
The standard approach to valuing investments computes the present value of expected cash flows at an appropriate discount rate. That is, a rate that reflects the riskiness of those cash flows.
Under this static methodology, managers can’t influence the cash flows of the project over time, as flexibility is not taken into account.
But in reality, adapting to uncertainty is a big factor in success.
The static NPV lacks the ability to efficiently capture uncertainty and flexibility. More specifically, its limitations include the following:
- Doesn’t always lead to good decisions: A conventional NPV above zero suggests the firm should take on the project. In reality? Not all projects with a negative NPV should be considered worthless immediately. Also, should a company accept an NPV of positive $1 for an initial investment of $1,000,000,000? Maybe not.
- Ignores the embedded option value: The traditional NPV rule assumes the investment opportunity disappears if it is not taken. In the real world however, most opportunities allow for some timing leeway. Only when a company invests in a project in the present, does it lose the ability to invest in that same project in the future. Thus, every project competes with itself delayed in time.
- Assumes reversibility: Another implicit assumption in DCF analysis is that the investment is reversible. Managers can go back in their decisions and recover the investment costs if the market conditions turn out worse than expected. In reality, most investment opportunities are irreversible, and the firm won’t be able to sell 100% of invested capital to other firms.
- Ignores managerial flexibility: Flexibility is at the heart of any business activity. Most importantly it has value. Why? Because as new information becomes available, managers make different decisions. The conventional DCF analysis ignores this. It assumes no adjustments, such as a project expansion or change in prices, are possible. But in actuality businesses can react to uncertainty and change the course of a project.
Using a probabilistic approach, such as Monte Carlo simulations, scenario analysis, and sensitivity analysis—which involve the probability-weighted average of cash flows under different scenarios to get an expected value—gives you more precise results.
These allow managers to study a distribution of possible outcomes, as opposed to focusing on a single most likely scenario.
However, they still ignore the managerial flexibility to respond to new information over time, unlike the expanded net present value:
Expanded NPV
An investment opportunity you don’t take today will not exist forever. Patents and leases that give you competitive advantages eventually expire. Competitors eventually catch up.
However, considering an investment opportunity disappears immediately if not undertaken is a lot more unrealistic.
Thus, instead of now-or-never, most projects are a now-or-later situation. Real options theory studies not only whether to invest but also when to invest.
The expanded net present value (ENPV) is a financial metric that factors in the value of real options into the valuation of an investment. What are real options?
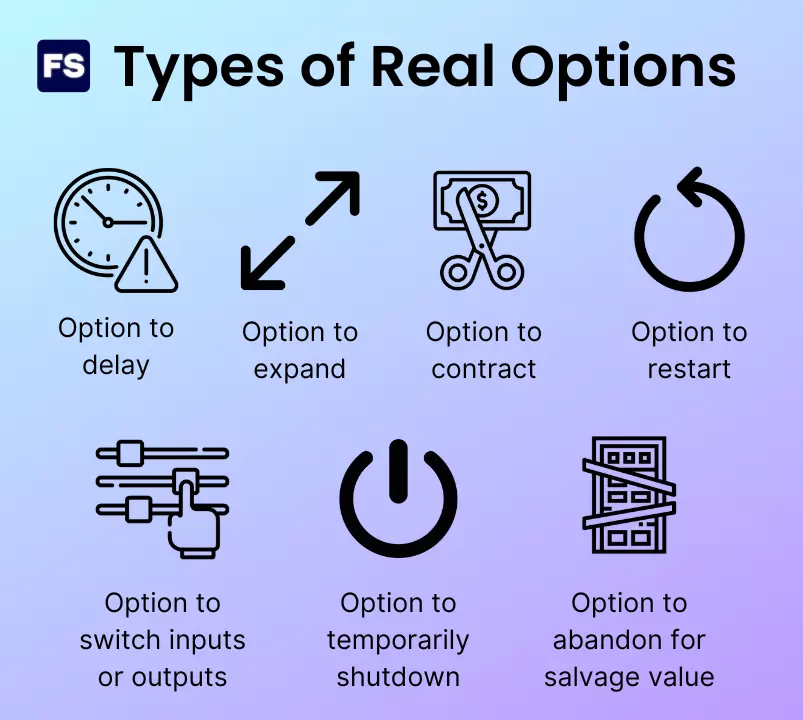
A real option is the right, but not the obligation, to undertake a business decision such as deferring, abandoning, expanding, or staging an investment.
Does this remind you of a certain financial instrument?
Real Options vs. Financial Options
Perhaps financial options, right?
This is why we call them real options. Because, unlike financial options, the underlying asset is a real-world capital project or asset (as opposed to a financial asset).
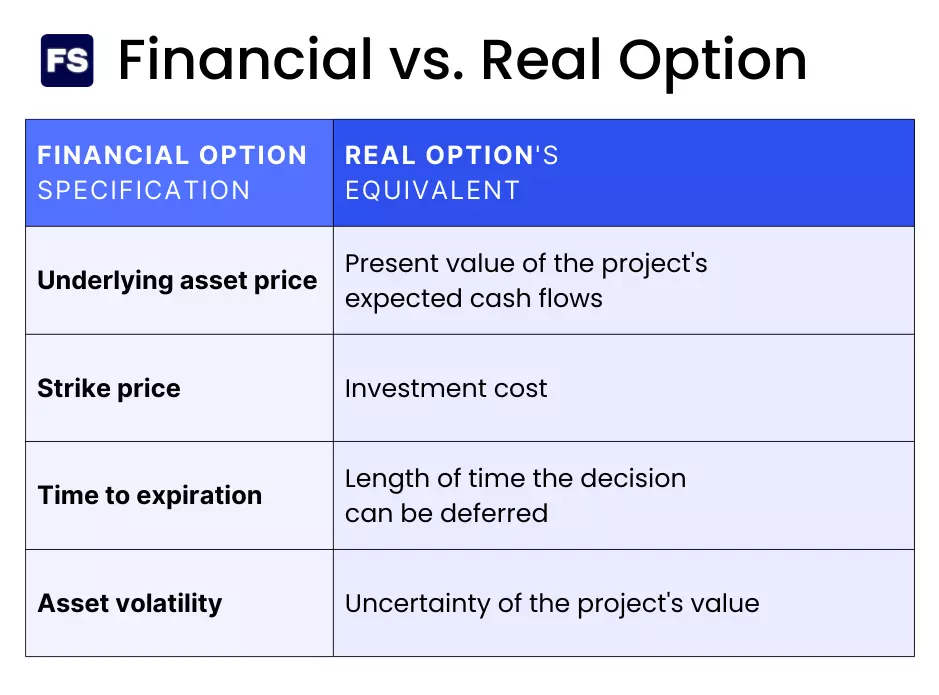
For example, a corporate investment opportunity is like a call option because the firm has the right, but not the obligation, to invest.
ENPV considers the potential for future growth and flexibility that comes with these real options.
Like the static NPV, a positive ENPV indicates the present value of the expected earnings the project generates is higher than the expected costs. And the firm should move forward with the project.
Now, when should you use the expanded NPV instead of the conventional?
Expanded NPV vs. Traditional NPV
Analysts use both the NPV and the ENPV in capital budgeting and investment planning to examine the profitability of an investment.
The standard NPV is appropriate for projects with low uncertainty or when it’s impossible to change the course of action as new information arrives.
On the other hand, real options valuation is better in situations where there’s high uncertainty, as it’s more likely that circumstances will change.
The main advantage of the expanded NPV is that it takes into account management’s ability to respond to good or bad news.
With the expanded NPV you can consider it’s possible to postpone the investment decision.
The traditional NPV on the other hand, assumes the investment opportunity is a now-or-never decision, and that if the firm declines the project now, it will never be able to do it in the future. The result? Undervalued investment opportunities.
But postponing a project is not the only type of real option:
So, how do you calculate the expanded NPV?
Expanded NPV Formula
It is equal to the net present value of the investment plus the value of real options:
Expanded (strategic) NPV = Static NPV + Option premium
Where:
- The static NPV is obtained by discounting the expected cash flows at a risk-adjusted discount rate.
- The option premium refers to the value of the flexibility that management has to alter the course of the project. How do you estimate it? Typically either through the binomial model, or the Black-Scholes model.
As you can see, the goal is not to completely ignore the static NPV. It is a necessary requirement for valuing projects through the strategic NPV framework.
Furthermore, in an investment where there’s no leeway or adaptability, the static NPV is equal to the expanded NPV. (The option premium is zero.)
Now, the expanded NPV can never be lower than the static NPV. Why?
Because that would mean the real option’s premium is negative. That’s never the case. No one will pay you to give you the right but not the obligation to an asset.
In other words, the opportunity to change strategies to profit more or cut losses will never have a negative value.
Expanded NPV Real World Example
Imagine a company has the opportunity to invest in an oil extraction project for a $55 million capital expenditure.
One year from today, the value of the investment will either move up to have an expected value of future cash flows of $90M or down to $30M (a binomial tree), depending on oil price fluctuations.
Assuming the up move and the down move have the same probability (50%) and an expected rate of return of 20%, the static NPV if the firm invests today is -$5M:
(90×0.50 + 30×0.50)/(1 + 0.20) = $50 million
The investment cost of $55M surpasses $50M, meaning the investment opportunity has a negative value.
Let’s say the company has a proprietary right (lease) to the oil project for a year. It can start the project either today or one year from now.
The opportunity to invest next year has a positive value. Why? Because oil prices may rise in the meantime, making the project profitable.
How do you determine the value of the option to defer the investment?
This option to wait is a call option. The underlying asset is the project and the strike price is the investment cost to be paid one year from today.
Using the Black-Scholes model, the value of the opportunity does not involve real-world probabilities. Instead, risk-neutral pricing and probabilities are used. These allow you to discount expected values at the risk-free interest rate.
Assuming a risk-free rate of 8%, the probability of an up move (qu) is 40%:
Knowing that the strike price is $55M (investment cost), let’s look at what happens at the expiration date of the call option in both scenarios:
- If oil prices rise and the project value goes to $90M, the intrinsic value of the option one year from now is 90 – 59.4 = $30.6M.
- If oil prices fall and the project value drops to $30M, it is below the strike price, meaning the call option is worthless.
Why $59.4M instead of 55? We assume the money is deposited earning the riskless interest rate until it’s time to invest one year from now. As a result, we multiply 55×1.08=59.4.
Therefore, the total value of the project including the option to wait is:
This implies the flexibility value of being able to delay the start of the project for one year thanks to the lease agreement is worth around 33% of the gross value of the project ($50M):
Option Premium = Expanded NPV – Static NPV = 11.33 – (–5) = 16.33
While this example follows unrealistic assumptions from the one-step binomial model, it signals the shortcomings of the traditional NPV calculation in the presence of managerial flexibility.
The Bottom Line
Here’s a recap of what you need to know about the expanded strategic NPV framework:
- The traditional NPV approach ignores the manager’s ability to adjust their original operating strategy whenever, as uncertainty is resolved, future events turn out different than what was expected initially.
- By contrast, the option-based framework recognizes the manager’s flexibility to adapt their future actions is part of the value of the project.
- A real option is a right (but not an obligation, unlike a forward contract) to modify an investment project in the future.
- The components of expanded NPV calculation are the static NPV and the option premium of real options.
There you have it! Hope this helps. Any questions? Leave them in the comments below.
