The VIX Index calculation takes the variance of two sets of SPX options with expiration dates between 23 to 37 days in the future. Then, it interpolates the variance between both. Finally, it takes the square root of that and multiplies it by 100. That’s the final VIX Index value.
Confused? There’s a lot to unpack here.
Let’s start by understanding the VIX and its purpose, before diving into the complex calculation used to derive its quote:
Understanding the VIX Index
The CBOE Volatility Index (VIX) is a measure of the expected stock market volatility for the next 30 days. It is based on the implied volatility of S&P 500 (SPX) option prices.
The VIX Index is the main benchmark for U.S. stock market volatility and investor sentiment. It is regularly featured in leading financial publications and business news shows, where many call it the fear index. Why?
Because it tends to rise when market conditions are uncertain and volatile.
Investors can use the negative correlation of volatility to stock market returns as a powerful tool for diversification. However, you cannot trade the VIX Index itself.
To go long or short volatility, you need to use a VIX futures contract, VIX options, or a VIX ETF.
Now let’s look at how the CBOE (Chicago Board Options Exchange) calculates the VIX:
The Initial VIX Formula
The generalized formula for the variance (σ2) used in the final VIX Index calculation is:
Where:
- T is the time to expiration, as explained in Step #2.
- F is the forward S&P 500 index level you get from SPX option prices (premium).
- Ki is the strike price of the ith out-of-the-money option. For calls Ki > K0 and for puts, Ki < K0.
- ΔKi is the average between the strikes immediately above and below Ki. This is explained in step #6.
- K0 is the strike immediately below F. (Explained in Step #5.)
- R is the risk-free interest rate. (Step #3)
- Q(Ki) is the midpoint of the bid-ask spread for each option with strike Ki, which is used in step #6.
This formula gives you the variance for one set of options. Why does the calculation use two sets of options?
Let’s break it down:
#1) Options Used in the Calculation
Similar to how stock indexes use the prices of a certain group of stocks to figure out their value, the VIX uses the prices (premium) of S&P 500 options to figure out its value. The question is, which options?
SPX put and call options with more than 23 days and less than 37 days to expiration. Why this specific range?
Because the VIX measures the 30-day expected volatility of the S&P 500. And using this range guarantees the VIX Index will reflect an interpolation of two points along the S&P 500 volatility term structure.
The S&P 500 volatility term structure is the relationship between the expected volatility of the S&P 500 index and the time until the options expire. It is graphed as a curve, with the time until expiration on the x-axis and the expected volatility on the y-axis.
This relationship is relevant to the VIX calculation because it reflects the market’s expectations of future volatility for different durations. Well, what duration do we want? 30 days.
Using options expiring between 23 to 37 days from now provides a stable and consistent view of expected volatility over the next 30 days.
This means the VIX formula uses two sets of options, which we call near-term options (more than—but close to—23 days until expiration) and next-term options (less than but closer to 37 days).
This is very important to remember. Basically, the VIX calculation is actually two calculations. In the end, they are counted together.
Why not just use one set of SPX options expiring exactly 30 days from now?
Because it results in a less stable view of implied volatility. These views can shift quickly, and using a single expiration date will not capture the changes as effectively as using a range of expiration dates.
Also, interpolation smooths out any discrepancies or biases in the prices of individual options, providing a more reliable gauge of market sentiment.
The VIX formula uses monthly and weekly SPX options. Standard monthly options expire on the 3rd Friday of each month. For the other Fridays? It uses SPX weekly options.
For example, on Monday, the 31st of October 2022, the SPX options used to calculate the VIX expired 25 and 32 days later:

Two days later, on November 2nd (Wednesday), the options expiring on Friday the 25th of November, were no longer taken into account. Why?
Because at that point, those options are precisely 23 days away from expiration. Therefore, they’re about to stop belonging to the 23-37 day range you’re looking for.
Instead, the options now used had expirations 30 days later (December 2nd) and 37 days later on December 9th (not in the picture above).
The near-term options are no longer used once they have less than 24 days left until expiration. What was previously the next-term expiration becomes the new near-term expiration, and the following longer expiration is added as the new next-term. This rollover happens every week.
#2) Precise Time to Expiration
Trading professionals are all about precision. This is why the VIX calculation measures time to expiration (T) in calendar days and divides each day into minutes.
The time to expiration follows this expression:
Where:
- MToday is the minutes left until midnight of the current day.
- MSettlement is the minutes from midnight to 9:30 AM ET if we’re dealing with a standard (monthly) SPX option (expiration every 3rd Friday). If we’re dealing with weekly options, MSettlement is the minutes from midnight until 4:00 PM ET.
- MOther is the total minutes in the days between the current day and the expiration day.
- MYear is the minutes in a year, which are 525,600 minutes.
This is important, as it is used throughout the whole calculation, along with the risk-free interest rate of return:
#3) Risk-Free Interest Rate
To take into account the time value of money, the VIX calculation uses the risk-free interest rate.
The time value of money refers to the fact you can invest a dollar you receive today and earn interest. Therefore, it is more valuable than a dollar received in the future.
By using the risk-free interest rate in the VIX calculation to account for the time value of money, the VIX Index reflects market expectations of future volatility more accurately.
What is the risk-free interest rate used in the calculation?
The risk-free interest rates are yields based on U.S. Treasury yield curve rates (Constant Maturity Treasury rates).
Remember:
The VIX calculation uses two sets of options—near-term and next-term. Thus, to take into account the time value of money, you may need to use two different interest rates.
To derive yields with maturities that correspond to the expiration dates of the relevant options, you apply a cubic spline to the CMT rates. A cubic spline is a mathematical function used to smooth out irregularities in a set of data points.
#4) Moneyness of the Options Selected
So, you know the expiration of both sets of options you’ll use in the VIX calculation.
Now the question is, are all options used, or just ITM options, or just OTM options? The answer:
The calculation uses at-the-money and out-of-the-money SPX calls and puts only.
In-the-money options are excluded.
However, those ATM and OTM options must have a bid different than zero.
Illiquid options are excluded.
This means that as volatility increases and decreases, the amount of option contracts with non-zero bids also changes. As a result, the number of options used in the VIX index calculation can change every month, every day, or even every minute.
Another thing about the non-zero bid rule:
If two consecutive OTM options have no bids, all options further OTM are not included in the calculation. Even if they have someone bidding for them.
For example, consider the following chain of OTM call options:
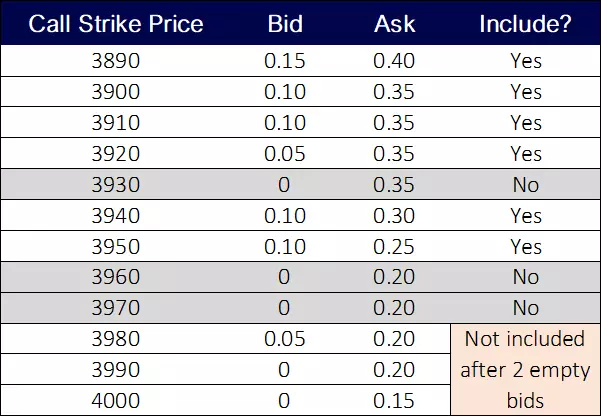
Notice how strikes 3980 is excluded even though it has a willing buyer.
This is because once two consecutive call options have zero bid prices, no calls with higher strikes are considered.
For puts it’s the inverse:
Once two puts with consecutive strike prices have no bids, puts with lower strikes are no longer included.
Keep in mind the VIX uses the midpoint of the quoted bid and ask prices for each option selected. Not the bid. The bid is just to determine if the option is included in the calculation or not.
#5) The First OTM Option Considered
The VIX calculation uses OTM options and one near ATM option. How do you determine the latter?
SPX prices don’t move in perfect chunks like what’s depicted in option chains’ strike prices.
There’s a special way to determine that first option considered. The one for which the strike is closest to being ATM. The strike from which all others that come after are considered (as long as they have bids).
This strike is the K0 used in the variance formula.
To determine it, you first calculate the forward SPX price (F).
You do this by identifying the strike price (S) at which the absolute difference between the call and put prices is smallest for both near-term and next-term expirations, and applying this formula:
Where:
- S is the strike price at which the absolute difference between the call and put prices is smallest.
- C is the call price (premium) of the option with strike price S. P is its put price. R is the risk-free rate, and T is the time to expiration.
Confused about the S? Take the following option chain as an example:
| Strike Price | Call | Put | Difference |
| 3880 | 27.40 | 18.60 | 8.80 |
| 3890 | 24.25 | 21.90 | 2.35 |
| 3900 | 22.10 | 24.15 | 2.05 |
| 3910 | 18.20 | 25.55 | 7.35 |
| 3920 | 15.15 | 27.85 | 12.70 |
The option price for the calls and puts is the midpoint of each bid-ask quote.
In this case, the strike price (S) used to calculate the forward index level is 3900, as the difference between the calls and puts in this strike is the smallest. The C is 22.10 and the P is 24.15.
You need to do this for both the near-term and next-term expirations. Meaning, assuming the option chain above is for the near-term options, you need to figure out the S for the next-term options as well.
The purpose of F is to determine K0, which is the strike price immediately below the forward index level (or equal to it). The K0 tells you exactly at what strike you start taking SPX options into consideration for the VIX calculation.
Continuing to follow the option chain above, if after calculating F it gives you a value of say 3898.5645 (this is a made-up number), then your K0 is 3890.
You need to then repeat the process for the option chain for the next-term expiration.
#6) Contributions of Individual Options
Next, select all out-of-the-money call options with strike prices above K0. And all out-of-the-money put options with strikes below K0. These are the options with strike Ki that go into the summation in the initial variance formula above.
What you want to do next is calculate an average of the price of all eligible puts and calls for both the near term and the next term. However:
It’s a weighted average. Not all eligible options have the same weight.
The closer to being at-the-money an option is, the more influence it has on the final result. Contributions decrease as you go further out-of-the-money.
This whole process is what’s depicted in the summation part of the VIX formula:
Where:
Basically, ΔKi is half the difference between the strike prices immediately above and immediately below K.
As you can see, the contribution of a single option to the VIX index value is proportional to ΔK and the price of that option, and inversely proportional to the square of the option’s strike price.
You calculate this for each eligible option in the near term and add the contributions together. Then, do the same for the next-term expiration.
Multiply the summation by the 2 and divide this by the corresponding time to expiration (T) for each term (as shown in the formula), and this part of the equation is done.
#7) Volatility for Near-Term and Next-Term
The hardest part is over.
All that is left is the second part of the equation:
This is relatively easy. Just plug everything into the formula and you should be good. Again, do it for both near-term and next-term.
Now, you just need to run the whole formula for both expirations. All the details about what you need were explained above.
This gives you the variance (volatility) for both sets of options.
#8) The Final VIX Index Number
With the 30-day variance of both expirations, you need to interpolate them.
After that, you transform it into a standard deviation by taking its square root. Standard deviations are the norm when talking about volatility. The VIX is no exception.
The final step is to multiply everything by 100.
This will give you the final VIX index value:
T1 is the time to expiration of near-term options. T2 is the time to expiration of the next-term.
σ1 and σ2 squared are the variances calculated in the previous step. Near-term and next-term respectively.
Now, the Ns?
- NT1 is the number of minutes until the settlement of the near-term options.
- NT2 is the minutes until the settlement of the next-term options.
- N30 is the number of minutes in 30 days (43,200).
- N365 is the number of minutes in a 365-day year (525,600).
For example, if the VIX Index is 23, it means a hypothetical S&P 500 option with 30 days to expiration has an annualized implied volatility of 23%.
Hopefully, you understand the basic idea behind the VIX and using OTM SPX options to price it means:
The CBOE uses the prices of out-of-the-money calls and out-of-the-money puts for two consecutive expirations.
What creates high or low VIX readings?
When the VIX level is high (let’s say over 30), then the prices of OTM options are high. This means the traders selling them want to receive a high premium for the risk that the market could go there.
Conversely, a trader buying must pay a high premium because the market has a good chance of expiring ITM and those options might actually be worth something.
Many people think a high VIX reading means the market risk of a large move down, hence the name fear index. This is wrong because the calculation takes into account the current prices of both calls and puts.
High VIX readings mean investors doing options trading are pricing in a significant chance of a sharp move in either direction, up or down.
When those same investors perceive a low chance of the market making big moves, the VIX level will be low.
Final Settlement Value for VIX Derivatives
If you trade VIX futures or options and hold them until expiration, the number calculated above is not what will determine the final result of your trades.
The final value used for the settlement of VIX futures and options is calculated using different rules. The CBOE uses the Special Opening Quotation (SOQ) of the VIX Index.
We won’t go over how exactly to calculate this value, but here are the key differences:
- The SOQ calculation uses a single set of SPX options. Unlike the VIX Index calculation, the SOQ calculation doesn’t involve interpolating the volatility of near-term and next-term options.
- The CBOE uses a special algorithm to determine the OTM options included in the calculation. There is no non-zero bid rule. All options within the range of strikes selected by this algorithm are used in the calculation, whether they’re liquid or not.
- Unlike the mid-quote prices used to determine the VIX Index, the SOQ computation uses the opening trading price of each of the chosen options. This opening price comes from a special opening auction conducted on days VIX derivatives settle.
You can follow the settlement value for the VIX through the ticker VRO.
Old VIX Calculations
The VIX was first introduced in 1993.
Originally, it was designed to measure the market’s expectation of 30-day volatility implied by at-the-money S&P 100 Index (OEX Index) option prices. It was an average of the Black-Scholes-Merton implied volatilities on 8 near-the-money options at the two closest maturities.
The main assumption of the Merton (1973) or Black and Scholes (1973) models is that the underlying asset price follows a geometric Brownian motion.
10 years later, in 2003, the CBOE along with Goldman Sachs updated the VIX Index to measure expected volatility in a new way. The new VIX Index was based on the S&P 500 Index, and estimated market volatility by aggregating the prices of SPX calls and puts.
In 2014, weekly options on the SPX were introduced. Thanks to this, the VIX could now be calculated with a set of options that made the 30-day target timeframe for expected volatility more precise.
This is the method used nowadays, and explained in this post.
VIX Formula FAQs
How is the VIX calculated?
The CBOE VIX is calculated using the weighted prices of SPX at-the-money and out-of-the-money options with expiration dates between 23 days and 37 days in the future. As a result, there are two sets of options in the calculation. After interpolating the variance of these two sets of options, transforming it into a standard deviation, and multiplying everything by 100, you get the VIX Index value.
What does the VIX actually measure?
The VIX Index measures the expected volatility of the S&P 500 Index for the next 30 days.
How often is the VIX calculated?
The VIX Index is calculated every 15 seconds during market hours and is published on the CBOE website.

Hi Hugo, thanks for the detailed explanation although I must admit i did still get lost at some point in your explanation. That being said, could I enquire if there’s any theoretical figure that the VIX calculation could be capped at? For instance, at a value of 100, what figures might need to fall in place at the actual option pricing and how realistic is that?