The geometric average monthly return tells you the average monthly return of an investment, assuming you reinvest the profits every month. Meaning, it takes into account the compounding effect. You calculate it by multiplying all the month’s growth factors together and raising that product to the inverse of the total number of months, after which you subtract 1.
That’s the gist of it.
For a more comprehensive guide on what is the geometric average, when to use it instead of the arithmetic average, and how it can help you analyze investments, keep reading:
What is Geometric Average Return
First of all, the words average and mean are the same thing. Average is used in Math, mean in Statistics. But they’re the same exact concept and I’ll use them interchangeably throughout this post.
Now that we’ve got that out the way, what is the geometric average return? Or geometric mean return?
The geometric average return is a way to measure the performance of an investment. It is most appropriate for investments that are compounded over many periods.
It is also appropriate for a series of volatile returns, as it takes into account the year-over-year growth or decline of the investment.
Now, how do you calculate the geometric average rate of return?
How to Calculate Geometric Average Return
To calculate the geometric average return you multiply all the returns and raise the product to the power of one divided by the length of the series of returns, then subtract one:
Where:
- r is the return for each period. Thus, (1+r) is the growth factor for that period. Another way to calculate the growth factor is to divide the absolute value of the investment at the end of the period by the value at the beginning.
- n is the total number of periods.
By raising everything to the power of 1/n and subtracting 1, you get the average growth rate for that period, which can be annual or monthly, or whatever you want.
This is the equivalent of using the nth root:
Obviously, the higher the investment return the better for you as an investor.
The geometric average return and the Compound Annual Growth Rate (CAGR) are the same exact thing:
Just like the geometric mean, the CAGR is the return on an investment assuming the profits are reinvested at the end of each period of the investment’s life span.
It may seem like there’s a difference because the CAGR takes the initial value and final value only, and assumes the investment grew at the same rate every year.
But this is the equivalent to the geometric average return where you into account each individual period’s true return, but then multiply everything. It works just like how a DuPont analysis decomposes the ROE. An expanded formula of the same thing.
Based on this, calculating the monthly geometric mean should be straightforward:
Geometric Average Monthly Return
It all depends on the data you have.
Most times we look at yearly data—so how to calculate geometric average annual return, right? In this case, you want to focus on monthly returns.
If you don’t have the investment return for each month in percentage already, you can use the absolute value of the investment at each period:
Following the same formula as above:
Where:
- n is the total number of months.
- (1+r) is the value of the investment at the end of the month divided by the value of the investment at the beginning of the month.
Wondering how to calculate geometric mean in Excel?
How to Calculate Geometric Average Return in Excel
You can use the GEOMEAN formula.
Here’s an example of an investment over 6 months:
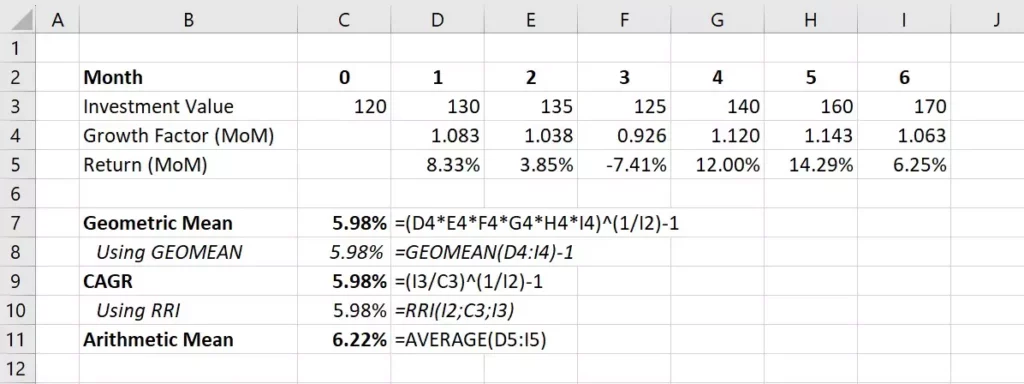
You start with 120 at time zero, and end with 170 six months later.
Couple things to notice:
- The growth factor and % returns are calculated as the MoM (month-over-month) change in the investment value. So the return as a percentage of the previous month’s value. For example, in month 4 the growth factor is 140/125=1.120.
- The GEOMEAN formula uses the growth factor and then subtracts 1, as opposed to using the % returns directly.
- The GEOMEAN function doesn’t work if you feed it negative values. And notice we have a negative return in month 3. However, since you use the growth factor—which is never a negative number—it doesn’t matter.
- The CAGR and the geometric mean are the same thing. But the arithmetic mean? It’s always higher.
Now, you may be wondering when to use the geometric mean…
Or even why use the geometric mean instead of the arithmetic mean, right?
Geometric Average Return vs. Arithmetic Average Return
The geometric average of a set of returns differs from its arithmetic average (also called arithmetic mean) because it considers the compounding of returns from period to period. The result?
The geometric mean is a more accurate measure of returns than the arithmetic mean. Why?
Because investment returns are linked to each other. They have autocorrelation (also called lagged correlation or serial correlation). Meaning, a big loss in one year implies you have less capital to generate returns in the following year. Thus, using the arithmetic mean to measure investment returns is misleading.
The arithmetic mean is simply the average of a sum of numbers. Here’s the arithmetic return formula:
It’s appropriate to use when you measure events that are independent of each other—such as average household income, average test scores, or the average debt level of companies in the tech sector.
If one family is wealthier, the next family’s chances of also being wealthy (or not) are unaffected, right? Same with test scores, one student performing well does not influence the score of another student. And companies in the tech sector operate independently, meaning the debt level of one company does not directly impact the debt level of another.
In finance, the arithmetic mean is not appropriate because annual investment returns are not independent of each other.
Most returns in finance are correlated, from stock returns to bond yields to risk premiums. The longer the time horizon, the bigger the impact of compounding, and the more appropriate the use of the geometric mean.
Geometric Mean vs. Arithmetic Mean: Which Is Higher?
For any given series of return observations, the geometric mean return is always smaller than the arithmetic mean return.
Why?
Because the geometric mean return takes into account the compounding effect of returns over time, which lowers the average return compared to the arithmetic mean return.
Key Takeaways (FAQs)
What is the geometric average of annual returns?
It’s the average annual growth rate of an investment over a specific period, considering the compounding effect. To calculate it, you need the initial value of the investment, the ending value, and the number of years involved. The geometric average of annualized returns is the same as the Compound Annual Growth Rate (CAGR).
How do you calculate geometric average return in Excel?
You can do it manually, so first you add 1 to each period’s return to get the growth factors. Then, multiply all the growth factors together and raise the product to the power of 1 divided by the total number of periods. Lastly, you subtract 1. Alternatively, you can use the GEOMEAN function with the growth factors and then subtract 1, or the RRI function with the initial and final investment value.
Can you convert arithmetic return to geometric return?
Not directly, but they’re calculated using the same information. The geometric return uses the growth factor for each period, which implies a percentage return for each period. The arithmetic return is the average of those percentage returns. Thus, if you have the information to calculate the arithmetic, you can also find the geometric return. And vice-versa.
