Second Derivative of Utility Function: Why Is It Negative?

The second derivative of a utility function is negative to reflect risk aversion and decreasing marginal utility. A negative second derivative implies a concave function, which illustrates that the more money you have, the less satisfaction you get from additional money.

But this doesn’t apply to money only. The more you consume a good or service, the less utility you get from an additional unit of that good or service.

Here’s an illustration that may help:

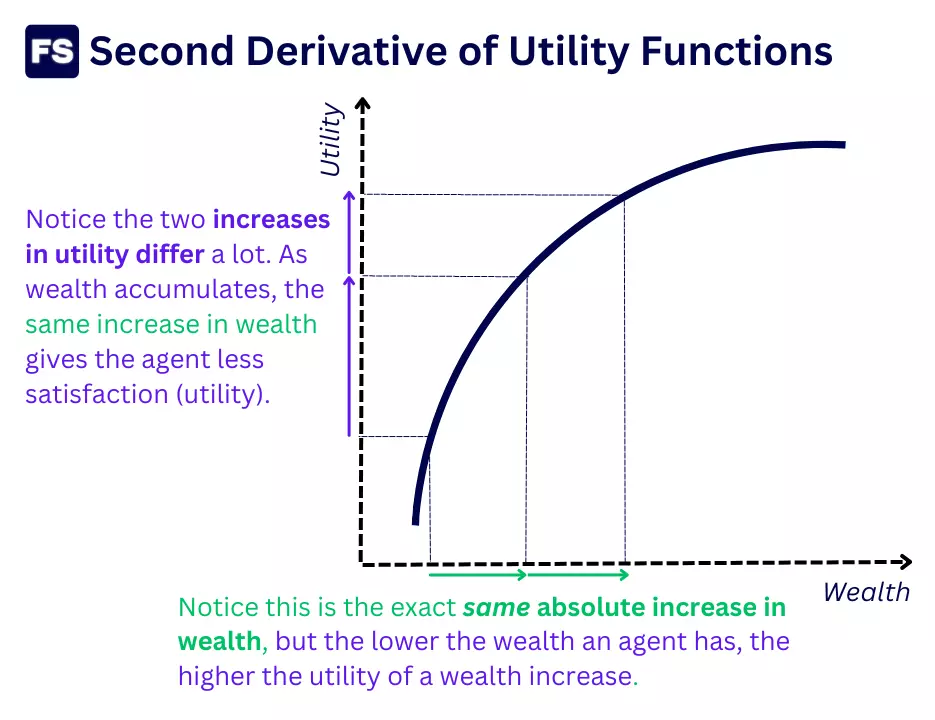
Still a bit confused? Don’t worry.

This post will help you understand everything you need to know about utility functions and their derivatives.

What Is A Utility Function

Utility functions are functions that map your preferences based on the satisfaction you get from a bundle of goods, services, or an investment.

In economics, utility is an abstract concept that means satisfaction, joy, benefit.

You denote utility with u and the utility you gain from preference x as u(x).

For example, let’s say your satisfaction from an orange follows u(orange), while the utility you gain from eating an apple is u(apple). If you prefer oranges over apples, the relationship between your utility functions is u(orange) > u(apple).

In finance and economics, utility functions allow you to compare whether one investor is more risk-averse than another and understand how an investor’s risk aversion affects his investment behavior and the composition of their portfolio.

Understanding Smooth Consumption

Humans prefer smooth consumption. What’s smooth consumption?

It’s balancing between spending for today’s needs and saving for the future.

For example, let’s say you have $30 to spend in one day on food. You get more satisfaction out of those $30 if you spend $10 on breakfast, lunch, and dinner each. Rather than spending the whole $30 on a fancy breakfast and being hungry the rest of the day.

Notice the amount you spend in both scenarios is the same—30 dollars. But the benefit, the satisfaction, the utility you get from them? It’s bigger when you optimize your consumption over time.

Basically, it is favorable to reduce consumption in states of high income in order to increase consumption in low-income states.

This implies marginal utility decreases as consumption increases.

Understanding Marginal Utility

“Marginal utility?”

Yes, that’s the satisfaction you get for each additional unit of goods, services, money, oranges, apples, whatever.

In general, you want a lot of something until you don’t.

For a poor person, the satisfaction of an extra $1,000/month is very high. But for a person making $300,000? It’s not as impactful, it doesn’t increase utility that much.

As wealth increases, the additional satisfaction you get from more wealth progressively decreases.

Now, how do you reflect this in a mathematical function?

It must be concave:

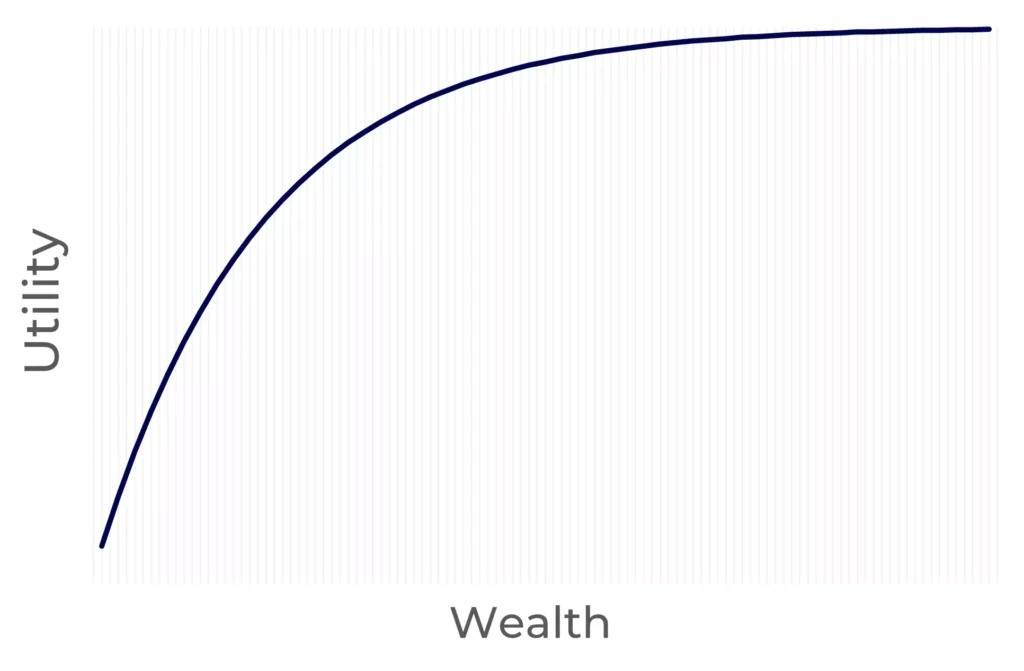
Utility functions are usually concave to reflect the decreasing marginal utility. And concave functions have negative second derivatives.

Let’s briefly remember what are derivatives to understand this:

Derivatives In Math Explained

You can think of the derivative of a function as its instantaneous rate of change.

The derivative of a function f(X) = Y tells you how a change in X relates to a change in Y.

If the derivative of a function u(w) is 5 when w equals 1000, it means that if w increases by 1 (from 1000 to 1001), u(1001) increases by 5. This means u(w+1) = Y + 5.

In math terms, when you find the derivative of a function, you’re finding a new function that tells you the rate of change of the original function at each point. The goal?

To help you understand how things are changing by looking at how a tiny change in a function’s input impacts its output.

Until now we talked about the first derivative, but there’s also the second derivative of functions. Let’s understand the distinction:

First Derivative

Within the context of utility functions of wealth, the first derivative is the rate of change in utility. In other words, how much additional satisfaction do you get when your wealth increases?

If the first derivative is positive, it means whatever you’re measuring (whether it is distance, height, or utility) is increasing. More wealth equals more utility.

If it’s negative, the utility you get from more wealth is decreasing.

If the first derivative is zero, it means wealth is not changing at that specific moment.

Second Derivative

This is the derivative of the derivative of a function.

So first you find the derivative of a function, then you find the derivative of that.

The first derivative measures the rate of change, while the second derivative measures how that rate of change itself is changing.

A linear function has a second derivative of zero (the function changes over time—implying the first derivative is not zero, but the rate at which it changes stays the same), a concave function has a negative second derivative, and a convex function has a positive second derivative.

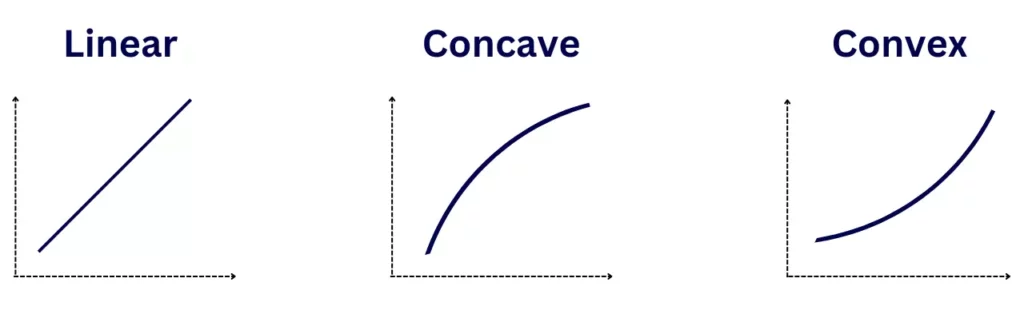
You can also think of utility through distance, speed, and acceleration:

• Imagine a function gives you distance (how far you’ve moved).
• The first derivative is speed, or how much your distance changes between two points.
• And the second derivative is your acceleration, or how your speed changes as you accelerate/decelerate.

In a concave function, speed is decreasing so acceleration is negative.

Now we’re positioned to understand the derivatives in a utility function:

Second Derivative Of A Utility Function

A realistic utility function reflects the human tendency to be risk-averse.

What’s risk aversion?

Put simply, it’s our tendency to prefer certainty over uncertainty—even when higher risk means higher expected return.

Risk aversion means you will avoid fair bets (meaning, whose expected value is zero).

You would rather get $100,000 with a 100% certainty than take a 50/50 chance of receiving either $200,000 or $0, right? Well, the expected value (sum of outcomes times their probability) of both options is $100,000.

Studying risk aversion allows us to understand the demand for a certain asset, which helps us price it.

Now, how do we arrange this in a mathematical function?

With a concave function (negative second derivative), as we’ve seen before.

This is because of the decreasing marginal utility, as it means positive deviations do not help as much as negative ones hurt.

For a risk-averse investor, the joy of making money is smaller than the pain of losing the same amount.

This implies investors may be willing to pay a premium (in terms of lower expected returns) to avoid uncertain outcomes and reduce their risk.

A concave function also means that in lower levels of wealth, the utility of getting more money is bigger. In contrast, as wealth increases, additional money brings less satisfaction.

Frequently Asked Questions (FAQs)