Quadratic Utility Function (Mean-Variance Preferences)

A quadratic utility function is a type of utility function used in economics and finance to describe a person’s preferences over different outcomes. In other words, how people make choices under uncertainty. The quadratic utility has special importance in finance as it implies mean-variance preferences.

The quadratic utility function implies increasing absolute risk aversion. This means people invest less money in risky assets as they get wealthier, a counterintuitive result.

In this post we’ll go over what is quadratic utility, its formula, purpose, and implications.

Ready? Let’s dive in:

What Is Quadratic Utility

Two concepts you need to understand very well before we continue:

• Risk aversion: How comfortable a person is with the risk of uncertain outcomes in exchange for a given return.
• Utility functions: Measures the satisfaction (happiness) you get from different bundles of goods, services, or investments. Utility functions are a way to measure risk aversion.

The purpose of these concepts? They help you quantify the demand for assets, therefore better estimating their price. This is essential for asset pricing and valuing future uncertain cash flows.

The quadratic utility function says an investor values different investment opportunities under uncertainty based on their mean wealth and the variance of their wealth.

This is what’s called mean-variance preferences—for any probability distribution of wealth, the expected utility depends only on the mean and variance of wealth, regardless of the probability distribution of the outcomes.

It is called quadratic because it is a quadratic function of the individual’s wealth or income (or unit of consumption, or anything you’d rather have more of).

A quadratic function is a polynomial function in which the highest exponent of a variable is two.

Like most utility functions, quadratic utility is a concave function. This means it assumes investors are risk-averse. Here’s why:

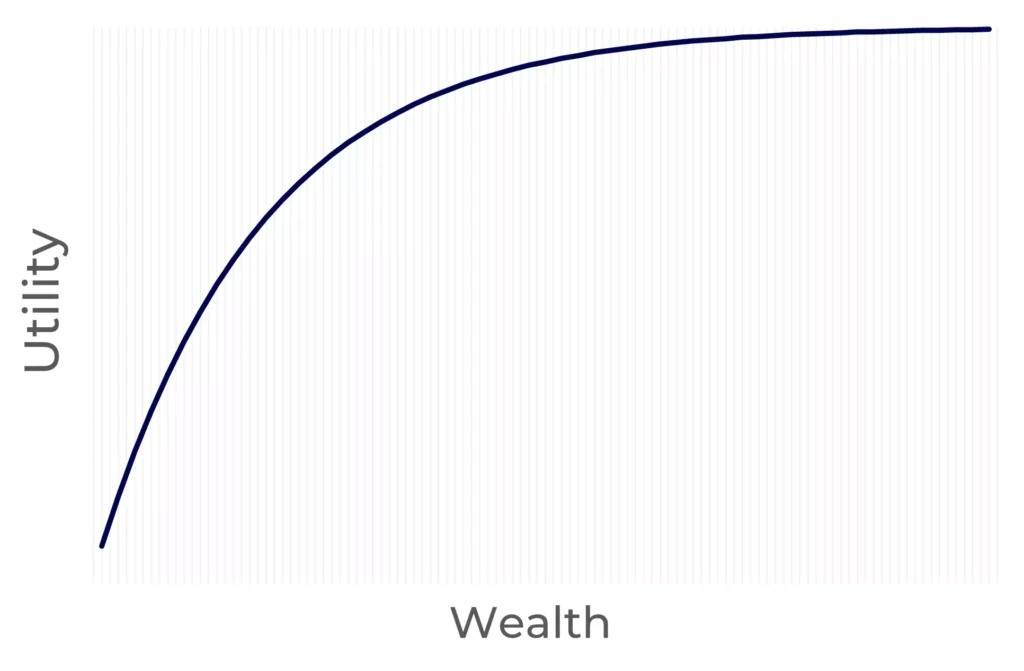
A concave function always has a negative second derivative. Which means it has decreasing marginal utility. What is this?

More wealth means more satisfaction. But the rate at which wealth brings more satisfaction decreases. A poor person will get more satisfaction from receiving an extra $100 than a person who is a millionaire already, right?

A concave function captures this human tendency—as you accumulate more wealth, you’re not as happy to get an additional dollar as you would be if you had lower wealth.

Moving on:

The quadratic utility function implies Increasing Absolute Risk Aversion (IARA).

This means the richer you are, the more risk-averse you are. Risky assets are inferior goods. A wealthy investor has less risk tolerance and as a result will invest less money in risky assets than a poor investor.

This is unrealistic.

It’s the same as saying a person with wealth of $1,000,000 is more afraid to lose $500 than a person with $1,000 to their name.

Quadratic Utility Formula

The mean-variance utility formula is the following:

\[u(w)=w-\frac{b}{2}w^2\]

Where:

• u(w) is the utility of wealth (w).
• b must be a positive number.

A unit of utility is not really something defined, but we know higher utility is better than lower. Utility means the satisfaction, happiness, or joy you get from an outcome. It’s not necessarily the same as money.

The quadratic function implies the individual’s marginal utility of wealth decreases as wealth increases, which is consistent with the idea of diminishing marginal utility.

Quadratic utility may only represent investors’ preferences over a limited range of wealth, and other utility functions may be more appropriate for different ranges of wealth.

Risk Aversion Coefficients

The risk aversion coefficient reflects the preferences of each investor in the face of uncertainty for a given utility function.

You calculate it using the first and second derivatives of the utility function:

\[u'(w)=1-bw \\ u”(w)=-b\]

There is the absolute risk aversion coefficient (α), which tells you how risk-averse an investor is. The higher the absolute risk aversion, the more favorable odds the investor demands to be willing to accept an investment.

You calculate it by dividing the second derivative of the by its first derivative:

\[\alpha(w)=-\frac{u”(w)}{u'(w)}\]

There’s also the relative risk aversion coefficient (ρ), which measures risk aversion irrespective of the level of wealth of the investor.

It is the absolute risk aversion coefficient times the level of wealth:

\[\rho(w)=w\alpha(w)=-\frac{wu”(w)}{u'(w)}\]

Hence, the absolute and relative risk aversion coefficients for the quadratic utility function are respectively:

\[\alpha(w)=\frac{b}{1-bw} \\ \rho(w)=\frac{bw}{1-bw}\]

Notice that when wealth (w) increases the absolute risk aversion coefficient also increases, showcasing the unattractive IARA property of the quadratic utility function.

FAQs (Frequently Asked Questions)